Ogromna je graja. Svi pričaju o veštalčkoj inteligenciji, mediji, teoretičari zavere, Ujedinjene nacije, estrada, pravnici, dizajneri, vojnici, umetnici... Prava dimna zavesa. Ni radnici se nisu toliko bunili kada sus e na početku industrijske revolucije pojavile složene mašine.
Oduvek su me nervirale skraćenice SOVNARKOM! I.T. A.I. Dobro I.T. to sam razumemo, nekada se to manje više zvalo birotehnika, ali A.I. ‘em intiligencija, ‘em veštačka, samo još da postane generalna. Kognitivna mašina primenljiva na sve procese. Multifunkcionalni više smerni manipulator.
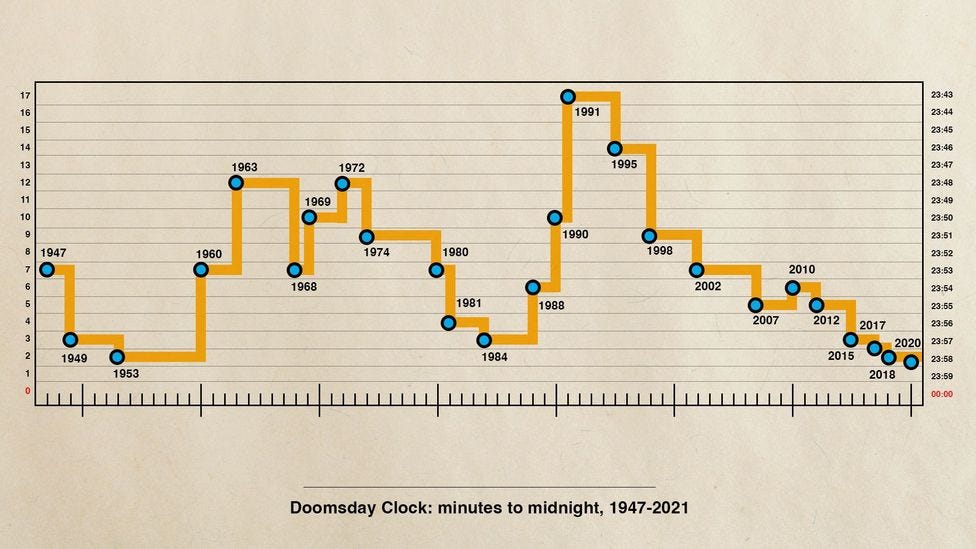
Čet GTP. Veliki jezički model koji se hrani svim i svačim., a zaštita intelektualne svojine i ličnih podataka? Kako radi pretraživač? Kako Google pronalazi naj kraći put iż tačke A u tačku B? Koja je to magija što skida pege, fleke i anomalije lica sa selfija, ili pravi od babe devojku? „Psihijatar se zaljubio u sopstvenu sliku ćaskajući sa Četbotom i zakazao mašini sastanak u motelu.” „Automatizovani robot ubio Iranskog naučnika! Mašinska intiligencija će uništiti, pisce pesnike i druge umetnike! Panila u paklu lažnih vesti. Digitalne monete. Bot klasteri. Zastarelost čoveka! Transhumanizam? Zašto nas plaše tim sokoćalima kada smo na evidentnu nuklearnu pretnju već potpuno otupeli? Ko nam baca prašinu u oči. Da li se „Doomsday Clock” pokvario ili će upravo da zazvoni. Razvoj, razvoj, ali kuda, ali čemu?
Da ne bih lutao po džungli bez kraja i početka sam se za razjašnjenje osnovnih pojmova obratio bliskom prijatelju koji se godinama bavi tom problematikom. On je jedan od viđenijih đaka Beogradske Matematičke gimnazije. Doktorirao je na dinamici fluida, a decenijama se bavi primenom mašpinske inteligencije u aitomatizaciji saobraćaja u uglednoj NASA laboratoriji. On me je, ne bez čuđenja, upitao šta đe mi to. „Eto, onako, nervira me sva ta graja, moram da razumem bar osnovne príncipe. Čist inat.” “Onda ti je naj bolje da negde pogledaš Markovljeve lance. Od toga je sve počelo. Naravno nije to jedina nit te teme aliu ti je dovoljno da osetiš o čemu se radi. Elegantna teorijska ruskog genija. Nemoj da te uplaše jednačine. Prilično su jednostavne ako pamtiš i pašljivo pratiš simbole kojima su pojave označene.” „Znaš i sam da nisam neki naročit matematičar. Postoji li neko jednostavno objašnjenje?”„Pa to ti i kažem, teorija skupova i nje neka visoka matematika, trebaju ti samo logika i koncentracija. Probaj, videćeš i sam.” „A zašto se oko toga onda diže tolika graja?” pitao sam „Jednostavno je. Markovljeva matematika je primenljiva na mnoga područja, pogotovo sada kada su baze podataka postale zaista velike, a lako pretražive, ne samo tekstualne, tu je ceo internet, ogromna baza fotografija i zvukova i pokretnih slika, karata, internet of tings, sve lako dostupno, pogodno za upoređivanje. Rrus je to otkrio zahvaljujući intelektualnoj radoznalosti, a pragmatični kapitalistički duh razvija dublje iż koristi. “ „I kuda to vodi?” Upitah. „Zavisi.” Reče mi prijatelj, “Od čega” Gotovo se pobunih na tako suv odgovor. “ Naravno od prirode ljudskog roda.” “Dobro, i šta to znači da li nam je odzvonilo.” On se nasmeja. „Ponašaš se kao naj gora TV voditeljka, postavljaš mi ono pitanje koje su počeli da zovu ’pitanje od milion dolara.” Ljudska istorija i nije ništa drugo nego poprište dobra i zla jer ni jedno ni drugo nikada nije u potpunosti povedilo.” A sat pokazuje devedeset sekundi do… Kazaljka nikada nije bila bliža, hoće li se zaustaviti?” On je ćutao. „U naj boljem slučaju će ogromnim naporom biti vrađena koji sat nazad. Uostalom ni zvezde nisu večne. Baci se na Markova pa ćemo posle pričati o tome. Došli su mi moleri pa moram malo da rasklonim...”
Bacih se na Rusa i evo u skraćenoj verziji onoga što sam uspeo da razaberem. Jedino još da dokonam otkuda baš sada mega saga o Openhajmeru.
Andrej Andrejevič Markov ( 1856 - 1922) je bio ruski matematičar rođen u Rjazanu. Studirao je na univerzitetu u Sankt Peterburgu. Godine 1886. postaje član Ruske akademije nauka. Najpoznatiji je po proučavanju u teoriji stohastičkih procesa. Njegova istraživanja su postala poznata kao Markovljevi procesi i obilato primenjena u raznim oblicima onoga što se danas zove mašinska inteligencija ili automacko učenje.
Osnovni pojmovi teorije verovatnoće su: stohastičnost, verovatnoća, slučajni događaj, prostor verovatnoća, slučajna veličina… Centralni pojam je slučajni proces. Slučajni proces je skup slučajnih veličina {X t |t∈T} definisanih na istom prostoru verovatnoća, pri čemu je t beskonačan skup. T je parametarski skup.
Parametarski skup možemo da zamislimo kao vreme. Ako je parametarski skup diskretan, onda se taj slučajni proces zove slučajni proces sa diskretnim parametrom (slučajni niz), a ako je parametarski skup neprekidan, naziva se slučajni proces sa neprekidnim parametrom.
Primeri slučajnih procesa:
Temperatura na nekom mestu merena svakog sata (temperatura u ovom slučaju predstavlja slučajnu veličinu, a sati parametarski skup)
Broj primljenih poruka od početka registrovanja do trenutka t (sama slučajna veličina je diskretna (broj poruka), a svakom trenutku možemo proveriti koliko je poziva stiglo, pa je parametarski skup neprekidan)
Kretanje cene akcije na berzi od nekog početnog trenutka do trenutka t (ovde je i slučajna veličina i vreme neprekidno).
Specijalna vrsta slučajnih procesa, nazivaju se procesi Markova i mogu se opisati ovako: "budućnost procesa zavisi samo od sadašnjosti (ili poslednjeg registrovanog trenutka), a ne i od prošlosti". Šta znači ovaj opis objasnićemo na sledećem primeru:
Svetlo u prostoriji može biti uključeno ili isključeno. Svakog sata neka osoba ulazi u prostoriju. Ako vidi uključeno svetlo, osoba ga isključuje sa verovatnoćom p , a ostavlja uključenim sa verovatnoćom 1 − p . Ako osoba vidi isključeno svetlo, ona ga uključuje sa verovatnoćom q , ili ostavlja isključenim sa verovatnoćom 1 − q . Zaključujemo da svetlo u sobi u trenutku n + 1 (posle n + 1 sati) zavisi samo od stanja svetla u trenutku n (posle n sati) i od toga da li će ga ta osoba isključiti ili uključiti (a ne zavisi od toga šta se desilo u prethodnih n − 1 trenutaka (sati)). To znači, da sva prethodna dešavanja vezana za uključivanje i isključivanje svetla nisu bitna, pa možemo da ih zaboravimo. Ovo svojstvo, naziva se Markovo svojstvo skupova.
onda je {X n |n ∈ ℕ} jedan slučajni niz koji može da uzme samo dve moguće vrednosti, tj. možese u tvrditi da se nalazi u dva stanja. Pri tome, nije bitno da li ćemo ta stanja obeležavati sa 1 i 2, sa " uključeno" ili "isključeno", već je bitno da znamo koliko ih tačno ima i sa kojim verovatnoćama se iz jednog od njih prelazi u drugo. To se može prikazati I ovako:

Markovljeve procese mogu postojati kao diskretani i neprekidani parametarski skupv, tj. mogu se odvijati ,,u diskretnom vremenu” ili ,,u neprekidnom vremenu”
Prvi rad Markov je objavio 1913. godine. Primer lanca sa dva stanja poznat je analiza dela teksta Puškinove poeme "Evgenije Onjegin". Markov je izvršio leksičku analizu tog poeme: izbacio je interpunkcijske znake, tretirao je prvih 20000 slova kao niz samoglasnika i suglasnika ( stanja kod tog lanca su bila suglasnik i samoglasnik) i odredio verovatnoće prelaska iz jednog stanja u drugo. Na primer, verovatnoću prelaska iz suglasnika u samoglasnik. Dobio je rezultat tako što je izbrojao koliko puta u tekstu za suglasnikom sledi samoglasnik, pa podelio sa ukupnim brojem prelaza I definisao matricu verovatnoća prelaska na osnovu koje je zaključio da se ona bitno razlikuje od matrice verovatnoća prelaska kod slučajno generisanog teksta (slučajno generisani tekst je nalik šeširu u kome se nalaze sva slova azbuke , iz koga vadimo jedno po jedno i vraćamo u šešir, a slova koja smo izvukli zapisujemo u niz). Eksperiment je matematička potvrda činjenice da jezik poezije, proze, kao i govorni jezik generalno, poseduju pravila i da nije reč o prostom ređanju slova. Metodologija Andreja Markova je osvetila probleme vezane za nezavisne događaje (kao što su, na primer, bacanja novčića i kockica), po sisteme povezanih događaja (gde od trenutnog stanja sistema zavisi šta će se i sa kojom verovatnoćom desiti sledeće). Markovljevi lanci su svuda oko nas i često se koriste u različitim oblastima. Primenjeni u drugim naukama, i uz podršku računara, pomažu, da se identifinišu geni u DNK, da se osmislle algoritmi za prepoznavanje govora i web pretragu.
Procesi Markova sa diskretnim vremenom
Kod procesa Markova sa diskretnim vremenom, parametarski skup je prebrojiv. Ako je skup stanja takođe konačan ili prebojiv pričamo o lancima Markova.
Razmnožavanje graška (lanac Markova sa konačnim brojem stanja)
Gen koji odredjuje da li je seme graška glatko ili naborano se sastoji od 2 alela: A (dominantni alel) I a (recesivni alel). Kada dodje do ukrštanja dve biljke, biljka potomak će dobiti po jedan alel (izabran na slučajan način) od svake od njih. Novodobijena kombinacija alela predstavlja genotip potomka. Genotip potomka može biti- aa, aA i AA. Istim postupkom se ukrštanje nastavlja kroz generacije.
Najduži neprekidni niz kod bacanja novčića (lanac Markova sa beskonačno mnogo stanja)
Baca se fer novčić i registruje da li je palo pismo (P) ili glava (G). Neka je X n najduži neprekidan niz G u trenutku n. Tada je {X n |n∈ ℕ} lanac Markova sa skupom stanja ℕ0 . Matrica verovatnoće prelaska bi izgledala ovako:
Kako je ova matrica beskonačne dimenzije, nije mogućr primeniti matrično množenje kao u prethodnom primeru. I ovaj primer može se prikazati grafički:
Klasifikacija stanja
Stanja se kod lanaca Markova mogu razlikovati i po tome koliko često (sa kolikom verovatnoćom) se lanac u njih vraća, tj. da li se to dešava skoro sigurno (sa verovatnoćom 1), ili sa nekom manjom verovatnoćom. Odgovor na to pitanje se zove klasifikacija stanja.
Procesi Markova sa neprekidnim vremenom
Neprekidni lanci Markova razlikuju od diskretnih po tome što pretpostavljamo da se promene stanja mogu desiti u bilo kom trenutku, a ne samo u diskretnim jedinicama vremena.
Verovatnoću prelaska iz stanja i (u trenutku s ) u stanje j (u trenutku t , t ≥ s ) definišemo sa p i j (s,t) = P{X(t) = j|X(s) = i} . Za homogene lance Markova sa neprekidnim vremenom važi p i j (s,t) = p i j (0,t−s) = p i j (t−s)
Primeri iz svakodnevnog života na koje je primenjiv lanac Markova u neprekidnom vremenu:
Proces rađanja i umiranja
Broj zečeva na kraju godine svakako zavisi od početnog broja zečeva. Ali zavisi i od inteziteta rađanja novih jedinki koji možemo da modelujemo (verovatnoća da se rodi nova jedinka u populaciji je veća što je trenutni broj jedinki u toj populaciji veći). Takođe, slično važi i za intezitet umiranja. Želimo da prognoziramo koliko će zečeva biti na kraju godine. Ako znamo broj zečeva na polovini godine (ili bilo kom drugom vremenskom trenutku) i znamo zakone po kojim se menjaju inteziteti rađanja i umiranja, za predvidjanje nam više nije bitan početni broj. Tada dobijamo novije podatke i svi oni prethodni nam više nisu korisni tj. ispoljava se svojstvo Markova.
Proces rađanja
Amebe se dele prostom deobom - kada ameba dovoljno izraste, ona se deli i obrazuje dve nove identične ćerke ćelije. Trenutak kada će se ameba podeliti zavisi od ispunjenosti nekih uslova, a vremenski interval potreban za ispunjenje tih uslova varira od amebe do amebe, što ovaj proces čini neprekidnim. Ovaj primer se razlikuje od primera sa zečevima zato što amebe ne umiru, već se na kraju svog života podele.
Sistemi masovnog opsluživanja
Sistem masovnog opsluživanja se sastoji od klijenata (onih koji treba da budu opsluženi) i servera (onih koji opslužuju). Klijenti traže uslugu u slučajnim vremenskim trenucima, i odlaze iz sistema kada budu opsluženi. (Činjenice da klijenti traže uslugu u bilo kom trenutku, a ne u unapred odredjenim diskretnim trenucima čini ovaj proces procesom Markova u neprekidnom vremenu). Klijenti mogu biti ljudi kojima treba pregled kod lekara, mušterije u frizerskom salonu, automobili na naplatnoj rampi, kamioni koji čekaju na istovar... Samim tim, serverom smatramo svakog radnika za šalterom, frizera u salonu, mehaničara u servisu, automat na naplatnoj rampi, mašinu u lancu proizvodnje... U svim tim sistemima, u zavisnosti od učestalosti pristizanja zahteva i dinamike opsluživanja, mogu se formirati redovi čekanja. S obzirom na to da kod mnogih od tih sistema stanje u budućnosti zavisi samo od trenutnog stanja sistema, brzine pristizanja novih zahteva, kao i od brzine opsluživanja postojećih, u ovoj oblasti lanci Markova imaju veliku primenu.
Neke od primena Markovljenih lanaca
Monopol:
Bacanjem kockice određujemo koliko naš pion napreduje po tabli, ali polje na kojem se nalazimo na kraju poteza zavisi i od početne pozicije, zato što je opseg zbirova vrednosti koje dobijamo bacanjem dve kockice limitiran (pion može ići od 2 do 12 polja unapred). Ovo je jedan model Markova gde skup stanja predstavljaju polja tj. države. Za svako stanje možemo izračunati verovatnoću prelaska na sva druga stanja do kojih možemo doći. Slična razmatranja važe i za mnoge druge društvene igre.
Krvne grupe:
Problem nasleđivanja krvnih grupa kod čoveka je komplikovaniji od ranije objašnjenog primera iz genetike (razmnožavanje graška), ali se zasniva na istom principu. Sad ćemo ovaj problem detaljnije objasniti:
Krv se deli na 4 krvne grupe u zavisnosti da li u eritrocitima postoje odredjeni protein. To su grupe: A, B, AB i 0. AB0 sistem krvnih grupa određuje gen koji se sastoji od 2 alela: A, B i 0. Od svakog roditelja se uzima po jedan alel. Dobijene kombinacije alela predstavljaju genotip deteta. Date kombinacije su (00, A0, AA, B0, BB, AB). Ako je X n genotip potomka u n-toj generaciji, onda je {X n |n ∈ ℕ} lanac Markova sa skupom stanja 00, A0, AA, B0, BB, AB. Odredićemo verovatnoću prelaska iz stanja A0 u sva ostala stanja. Verovatnoća da se dobije genotip 00 jednaka je verovatnoći da se od oba roditelja uzme alel 0, tj. 1/2 * 1/2 = 1/4 . Verovatnoća da se dobije genotip A0 jednaka je verovatnoći da se od jednog roditelja uzme alel 0, a od drugog alel A, tj. 1/2 * 1/2 + 1/2 * 1/2 = 1/2. Verovatnoća da se dobije genotip AA jednaka je verovatnoći da se od oba roditelja uzme alel A, tj. 1/2 * 1/2 = 1/4 . A verovatnoća da se dobije bilo koji drugi genotip je 0. Sledeća matrica prelaska prikazuje koju krvnu grupu i sa kojom verovatnoćom može imati dete, ako roditelji imaju istu krvnu grupu.
Lanci Markova u muzici:
U mnogim slučajevima, muzika služi kao pratnja drugim oblicima umetnosti i aktivnosti, kao što su filmovi, video igre, pozorište, pozadinska nuzika u restoranima i muzejima… Dokazano da postoji veza između muzike i emocije, pa muzika u ovim slučajevima služi da podstakne raspoloženje koje neko želi da prenese ljudima. Uz pomoć proceduralnog generisanja sadržaja (polje u nauci koje algoritamski stvara nasumični, slučajni sadržaj ili umetnost u okviru postavljenih ograničenja koje mi zadajemo), mogu se kreirati sistemi za slučajno generisanje muzike koja odgovara željenom raspoloženju. Da bi proceduralno generisana kompozicija izazivala željeno raspoloženje u određenom trenutku, za svako raspoloženje se zadaju različite vrednosti parametara koji se upotrebljavaju za svaki aspekt kompozicije (tempo, visinu tonova, vrednosti nota, dominantnost akorda i melodiju nota). Tako da budući tok melodije zavisi od trenutne melodije i od pravila koje smo malopre pomenuli, pa je u pitanju lanac Markova.
Iako sam odustao od matematike još u trećem razredu gimnazije proveo sam više od dvadeset vrelih ljulskih noći da bih zapamtio simbole koji opisuju pojave i u visokoj meri razumeo Markovljevu teoriju korak po korak. Verovatno bi mi trebalo još toliko vremena da sve trajno memorišem i mogu da je matematički formulišem bez podsetnika na papiru, obzirom na poodmakle godine. Priznajem da sam ponosan na sebe, a siguran sam da bi se i moj otac, koji je bio odličan statističar, napokon ponosio mnome i oprostio mi što sam svoje vreme traćio na uzaludne pokušaje da se bavim filmskom umetnošću u okolnostima u kojima je verovatnoća za to jednaka nuli. Računar bi sve ovo procesirao i zapamtio mnogo brže, zapravo u trenutku. On to non stop i radi, ali za razliku od mene on nikada neće biti ponosan, niti će imati uspomene na pokojnog oca. Odavno postoji rasprava o tome '‘Da li androidi sanjaju električne ovce” međutim čini se da je ona ipak fatamorgana koja se nam izmiče pre svega zahvaljujući čovečnošću čoveka, u čemu i jeste naj veća ludska veličina.
Ukoliko vas je moj napor da utrošim dokono vreme iole inspirisao da učinite nešto za sebe, ili čovečanstvo, bez obzira koliko se osećali slabima, pokušajte da preduzmete neki krupan i beskoristan intelektualni napor kojim će te iznenaditi sebe. To je jedini način da se kazaljka “Doomsday časovnika, vrati u nazad koji sat, ako se već ne može zaustaviti. Valjda još nismo postali dinosaurusi.
Priredio: Milan Peca Nikolić