NAJLEPŠA JEDNAČINA

Mamatematičke konstante u idealnom jedinstvu

Čitavog života slušam kako je matematiku teško razumeti i stalno ubeđujem ljude da mi dozvole da im objasnim - pošto sebi laskam da mogu prilično dobro da drugima pojasnim čak i komplikovane teme, a pritom verujem da je matematiku ubedljivo najlakša od svih mogućih tema pošto je krajnje logična. Teže je shvatiti, recimo, nečiju motivaciju, ili neko umetničko delo. Tu ti treba neka intuicija, imaginacija, empatija... A za matiš ti ne treba ništa, sem elementarne inteligencije.

Ipak, niko mi ne da da mu objašnjavam matematiku! Decu sam jurio po kući, ali su uvek bili brži da pobegnu. Žena, koja neguje umetnički identitet (a na njenoj Akademiji važila je poslovica “glup kao skulptor”) i dalje prepričava po žurkama da sam joj tvrdio da čak i nju mogu da naučim matematiku za nedelju dana. Njen odgovor je uvek bio: “Nisam se udala da bi me ti gnjavio”. Tako da mi evo preostaje samo papir, koji trpi svašta, pa možda ipak nekako uspem da ‘navatam’ ponekog naivnog čitaoca...

Čovek može da počne odakle god hoće, a ipak će na kraju stići do celokupne matematike. Evo, ja ću da počnem od jednačine koju smatram najjednostavnijom, pa tako i najlakše razumljivom u matematici:

Ako ste ovo shvatili, onda sigurno možete da naučite matematiku. Možemo ovde čak i da stanemo jer već znate sve što treba, samo što toga niste svesni. Kada sam ovo rekao sinu, odmah je odgovorio: “Dobro, stajemo…”. Vama neću da dozvolim to zadovoljstvo. Pa ću da nastavim da objašnjavam šta se ustvari ovde krije, a krije se ideja da je matematika neki niz ‘zamena’ koje se na kraju svode na odredjene brojeve. U ovoj jednačini gore, čovek može da zameni -1 ili +1 sa beskrajno mnogo nekih drugih brojeva ili simbola, koji se medjusobno nalaze u specifičnim relacijama, a da se i dalje zadrži validnost jednačine. Uslov je da određenim kalkulacijama to ‘drugo’ na kraju može da se svede na -1 ili +1.

Evo jedan primer. Jedna od najčuvenijih, a sigurno najelegantnijih jednačina u matematici izgleda ovako:

Nazvana je ‘Ojlerov identitet’. Ovde je očigledno (i zato nemojte da mi kažete da vam je ovo teško ili zbunjujuće) da je e^iπ jednako -1. Ko su junaci ove formule? Zašto su za matematiku značajni e, i, kao i π ? Da bi ste to shvatili ispričaću vam priču o svakome od njih.

π je konstanta koja opisuje odnos oboda kruga i njegovog prečnika. Verovatno se rodilo u pradrevna vremena, par hiljada godina pre nove ere, iako tada još uvek nije dobilo ime, niti su izračunali njegovu pravu vrednost. Vavilonci su pretpostavljali da mu je vrednost oko 3,125. Egipćani su ga računali kao rezultat razlomka 256/81, što je 3,16045, a ispostavilo se da je istina negde u sredini, pošto je u pitanju iracionalni broj, čija je približna vrednost 3.141592653589793238462643383279502884197…Ime mu je dao engleski matematičar Viliam Džons 1706. godine.

π je značajno za razumevanje jednog od najstarijih i najvažnijih izuma čovečanstva – točka. Ako se zapitate koliki put prelazi točak dok ne obrne jedan pun krug – pod uslovom da prečnik točka postavite kao mernu jedinicu – videćete da je taj put ukupno 3,14 prečnika, ili tačno jedan π.

Zbog toga se pojavljuje u svim osnovnim formulama vezanim za krug: formuli za obod kruga koja je 2rπ i formuli za površinu kruga, koja je r²π (pri čemu je r poluprečnik). Pošto je u Kosmosu sve kružno, eliptično i sferično, od oblika zvezda, putanja planeta, pa do forme celokupnog Univerzuma, koji se može predstaviti kao jedna velika lopta koja se širi, π se pojavljuje u gotovo svim matematičkim formulama koje opisuju ove oblike i ova kretanja. Sferna geometrija je bez π nezamisliva. Drugim rečima, kad god se otvori matematički orman Kosmosa, π počne da ispada u velikim količinama.

i je trebalo da bude najbolji dokaz da matematika nema veze sa realnošću, već je “umetnost radi umetnosti”. Ljudi su vremenom shvatili da postoje celi brojevi, ali i oni koju su izvedeni iz razlomaka (racionalni brojevi). To su dva tipa brojeva koje su priznavali Pitagorejci, kojima je bilo neshvatljivo da mogu da postoje i iracionalni brojevi, a, ne daj bože, transcendentalni brojevi, to jest brojevi koji nemaju jednoznačnu vrednost, već se njihova vrednost mora izračunavati do u beskonačnost. π je tipičan primer jednog iracionalnog broja, kome se, iza zareza, mora dodati beskonačno mnogo brojeva da bi se kompletno precizno utvrdila njegova vrednost. Ipak, u odbranu takvih brojeva, može se reći da su oni barem ‘realni’ to jest da se mogu upotrebiti za opis kontinualnih jednodimenzionalnih entiteta (recimo, dužina ili temperature).

i opisuje jednu sasvim drugu, totalno ‘izmišljenu’ kategoriju brojeva, koji su zbog toga nazvani imaginarnim. Nastao je rešavanjem, na izgled, ‘nemoguće’ jednačine:

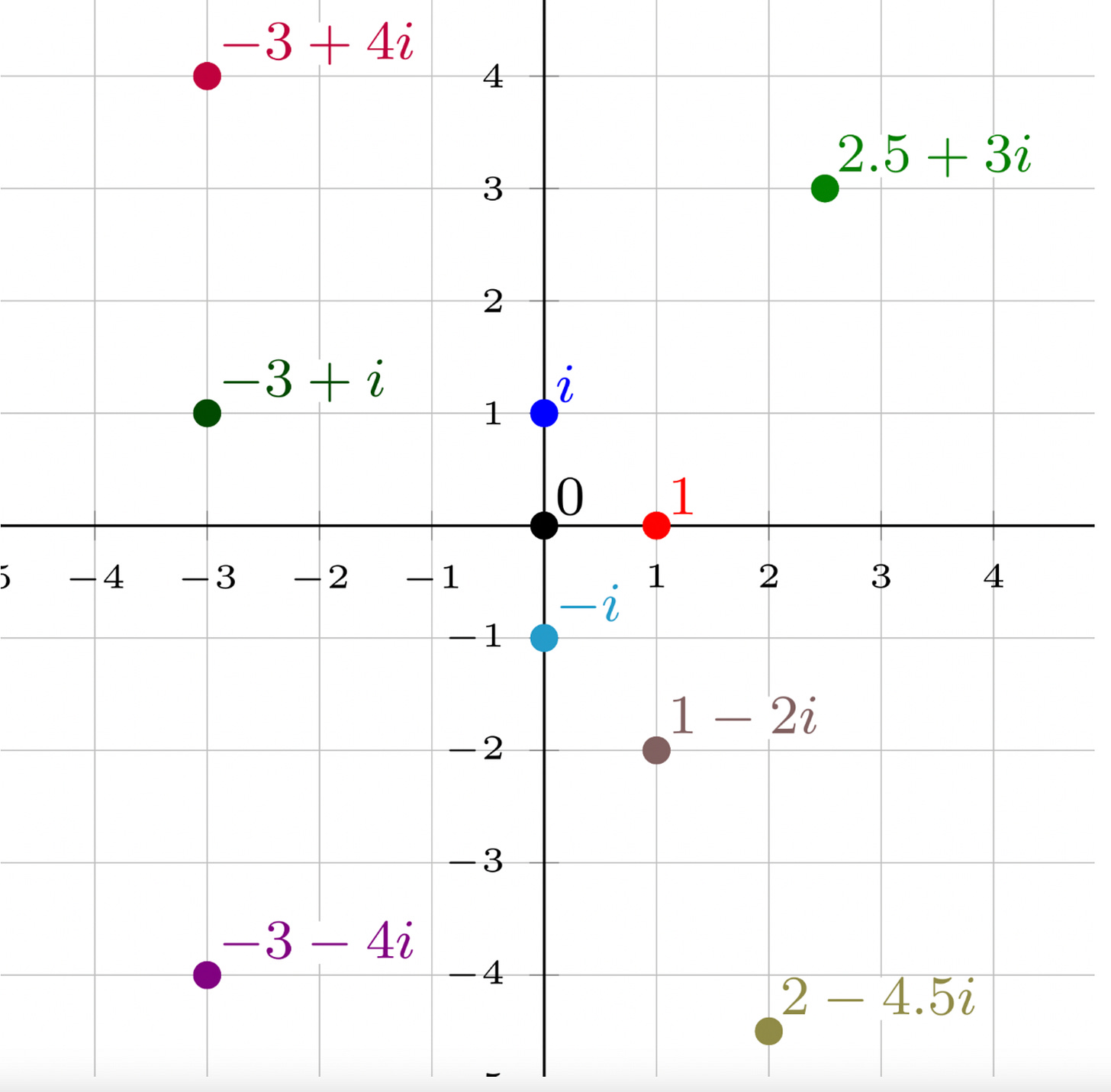
Ova jednačina je izgledala nemoguće, jer ne postoji realni broj čiji kvadrat može da ima vrednost -1. Zbog toga je takav broj jednostavno izmišljen i obeležen slovom i. To je omogućilo da se generiše novi beskonačan niz brojeva koji predstavljaju umnožak izmišljene konstante i i nekog realnog broja, pa je taj niz brojeva nazvan ‘imaginarnim’. A to je, opet, omogućilo sintetizovanje teorije brojeva kao ‘kompleksnih’ brojeva. To možemo razumeti ako posmatramo sledeći koordinatni sistem, čije su jedinice mere 1, -1, i, kao i -i:

Svaki broj se može predstaviti kao tačka u ovom prostou, koja se sastoji od dva parametra: vrednost na x i na y skali. Tako se broj 5 može predstaviti kao: (5 + 0i) a sam broj i kao (0 + i). Ovi brojevi se, naravno, nalaze na osama, i oni su velika manjina u odnosu na sve moguće brojeve koji se nalaze negde između u ovom prostoru i mogu da se predstavi kao (3 +2i), (6,7 - 4,2i) i tako dalje.

Vremenom se ispostavilo da imaginarni brojevi nisu toliko imaginarni koliko se u prvom trenutku mislilo i da su čak neophodni za izračunavanja nekih realnih problema, kao što su problemi u kvantnoj mehanici, elektrodinamici, finansijskoj matematici, optičkom inženjeringu i tako dalje. Konstanta i, za koju smo verovali da smo je izmislili na jedan potpuno veštački način, ispostavila se kao krucijalno važna za matematičko kvantifikovanje procesa koji utiču na generisanje same strukturu materije, kao i štošta drugo.

Da bi se shvatio smisao i značaj konstante e, potrebno je krenuti od onoga što svaki učenik shvati u prvih par razreda osnovno škole: a to je da su sabiranje i oduzimanje daleko prostiji i zahtevaju manje vremena nego množenje i deljenje. Kad bi samo nekako mogli da svedemo množenje i deljenje na sabiranje i oduzimanje – gde bi nam bio kraj! Srećom, mi danas ne moramno da se time bavimo, pošto su matematičari još davno otkrili da komplikovane računske operacijne mogu da se svedu na prostije. Množenje i delenje se nalaze u osnovi ‘geometrijske progresije’, dok su sabiranje i oduzimanje u osnovi ‘arimetičke progresije’.

Dole je jedna aritmetička progresija. Dodajući isti broj (u ovom slučaj broj 1), pravimo neki aritmetički niz:

A ovo je geometrijska progresija. Množenjem istim brojem (u ovom slučaju, brojem 2) dobijamo neki geometrijski niz:

Ova dva niza možemo da postavimo u jednu tabelu, što će nam pomoći da koristimo jednostavnije računske operaciju umesto komplikovanih.

To izgleda ovako. Uzmimo da hoćete da pomnožite 8 i 16. Pogledate u tabeli aritmetičkog niza koji su brojevi na njihovom mestu. To su brojevi 3 i 4. Kada ih saberete dobijete 7. Sada pogledate koji broj stoji pored sedmice u tabeli geometrijske progresije. Videćete broj 128. To znači da je 8 x 16 = 128. Prava magija! Sabiranjem 3 + 4 mogli ste da zaključite koji je rezultat množenja 8 x 16. To može da se primeni i na više od dva broja. Recimo: 2x4x16 izračunavate tako što saberete 1+2+4, što je sedam. Pored sedmice levo vidimo broj 128. To je, dakle, rezultat množenja 2x4x16.

Problem koji ovde odmah uočavamo je da ova tabela omogućuje množenje i deljenje nekih brojeva a ne i nekih drugih. Recimo, u levoj tabeli nema broja 3, kao ni brojeva 11, 12, 13 i tako dalje. Ispostavilo se, međutim, da je tu samo problem u broju 2, kojim smo množili brojeve da bi dobili geometrijski niz. Ako bi množili brojem 1,000001 (ili 0,999999) ne samo da bi mogli da ovako izračunavamo sve prirodne brojeve, već i racionalne, pa čak i iracionalne brojeve. To je omogućilo kreiranje mnogo detaljnije tabele.

Gore se vidi deo tabele koji pokazuje da, ovakvim množenjem, već pre nego što smo u geometrijskoj progresiji stigli do broja dva, mi smo u arimetičkoj stigli skoro do 700 000. Ta vrednost, sa desne strane, nazvana je logaritmom broja koji vidimo sa leve strane. Pošto je ovako generisanih brojeva jako mnogo, logaritmi su predstavljani kao čitave knjige sa tabelama, nazvane ‘logaritamskim tablicama’.

Logaritamske tablice iz 1803. godine

Ukoliko sada čovek hoće da pomnoži, recimo, 1,999988 sa 1,999992 kao i 1,9999998, što je prilično komplikovano, samo treba da sabere:

693142

694144

+ 693147

Štagod da dobijete (a ovo je lako sabrati), samo pogledate levo koji broj stoji u geometrijskom nizu pored broja koji ste dobili. Taj broj je rezultat onog komplikovanog množenja. Menjanjem brojeva koje koristimo za generisanje aritmetičkog niza dobijamo različite logaritamske tablice, od kojih su neke korisnije za rešavanje jednih a druge za rešavanje nekih drugih računskih operacija.

Nije dugo trebalo da matematičari shvate da su logaritni rešenje za problem eksponencijalnih funkcija. To se desilo u 18. Veku. Dole se nalazi primer hiperbolične funkcije.

Tu se može uspostaviti korelacija odnosa distance koja sledi geometrijsku progresiju i površine, koja sledi aritmetičku.

Iz čega se moglo zaključiti da su logaritmi ne samo dobar trik za pretvaranje teških u laka izračunavanja, već suštinski matematički entitet, koji je neposredno vezan za rešavanje eksponencijalnog računa. Tako je utvrđena sledeća zakonitost: ako je y = n^x onda sledi da je log_ny = x. Odjednom su komplikovane eksponencijalne operacije mogle da se rešavaju nalaženjem rešenja u logaritamskim tablicama!

Posebno korisnim pokazali su se logaritmi koji kao ‘bazu’ (n u gornjem primeru) koriste iracionalnu konstantu e ≈ 2,71828 18284 59045 23536 02874 71352... Ti logaritmi se dobijaju kada se aritmetička progresija kreira dodavanjem veoma malog broja 0,00001, što ih i čini primenjivim na ‘krive’ funkcije. Specifičnost konstante e je da tangenta funkcije y = e^x identična vrednost visine (vrednosti na y osi koja iznosi tačno 1, pri x=0), pa se lako može preraditi u osnovu za sva eksponencijalnih izračunavanja.

Ispostavilo se da je ova konstanta ključna za opisivanje skoro svakog prirodnog rasta, kvantifikovanje promena temperature, radioaktivnog raspada, eksponencijalnog razvoja populacije (recimo, bakterija), nuklearnih reakcija, a takođe i za izračunavanje verovatnoća, kao i kamata.

Sada, kada smo upoznali sve konstante sabrane u Ojlerovoj jednačini nadam se da možemo da shvatimo njenu eleganciju kao i značaj. Ona povezuje tri najvažnije matematičke konstante (π, i i e) kao i dva najvažnija broja (0 i 1) jedinstvenom formulom, čime najbolje demonstrira konzistentnost kosmičkog logosa, i beskrajno bogatstvo mogućih kvantitativnih operacija koje su, na kraju krajeva, laički gledano, izvedene iz proste činjenice da kada nešto oduzmeš od sebe samog dobiješ – NIŠTA.

Ako ste izdržali sa čitanjem ovog teksta do kraja sigurno imate sposobnost da razumete matematiku. A možda i sklonost… Ne zavaravam se, doduše, da će neko od ‘mojih’ ovaj tekst udostojiti sa više od ‘ovlaš’ prelistavanja.

Autor: Slobodan Simović